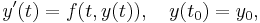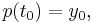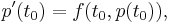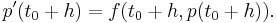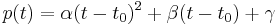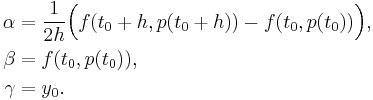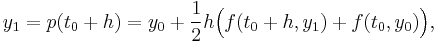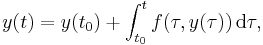Collocation method

In mathematics, a collocation method is a method for the numerical solution of ordinary differential equations, partial differential equations and integral equations. The idea is to choose a finite-dimensional space of candidate solutions (usually, polynomials up to a certain degree) and a number of points in the domain (called collocation points), and to select that solution which satisfies the given equation at the collocation points.

Ordinary differential equations

Suppose that the ordinary differential equation

$y'(t) = f(t,y(t)), \quad y(t_0)=y_0,$

is to be solved over the interval [t₀, t₀ + h]. Choose 0 ≤ c₁< c₂< … < c_n ≤ 1.

The corresponding (polynomial) collocation method approximates the solution y by the polynomial p of degree n which satisfies the initial condition p(t₀) = y₀, and the differential equation p'(t) = f(t,p(t)) at all points, called the collocation points, t = t₀ + c_kh where k = 1, …, n. This gives n + 1 conditions, which matches the n + 1 parameters needed to specify a polynomial of degree n.

All these collocation methods are in fact implicit Runge–Kutta methods. However, not all implicit Runge–Kutta methods are collocation methods. ^[1]

Example

Pick, as an example, the two collocation points c₁ = 0 and c₂ = 1 (so n = 2). The collocation conditions are

$p(t_0) = y_0, \,$

$p'(t_0) = f(t_0, p(t_0)), \,$

$p'(t_0%2Bh) = f(t_0%2Bh, p(t_0%2Bh)). \,$

There are three conditions, so p should be a polynomial of degree 2. Write p in the form

$p(t) = \alpha (t-t_0)^2 %2B \beta (t-t_0) %2B \gamma \,$

to simplify the computations. Then the collocation conditions can be solved to give the coefficients

$\begin{align} \alpha &= \frac{1}{2h} \Big( f(t_0%2Bh, p(t_0%2Bh)) - f(t_0, p(t_0)) \Big), \\ \beta &= f(t_0, p(t_0)), \\ \gamma &= y_0. \end{align}$

The collocation method is now given (implicitly) by

$y_1 = p(t_0 %2B h) = y_0 %2B \frac12h \Big (f(t_0%2Bh, y_1) %2B f(t_0,y_0) \Big), \,$

where y₁ = p(t₀ + h) is the approximate solution at t = t₀ + h.

This method is known as the "trapezoidal rule." Indeed, this method can also be derived by rewriting the differential equation as

$y(t) = y(t_0) %2B \int_{t_0}^t f(\tau, y(\tau)) \,\textrm{d}\tau, \,$

and approximating the integral on the right-hand side by the trapezoidal rule for integrals.

References

^ Ascher, Uri M.; Linda R. Petzold (1998). Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Philadelphia, USA: SIAM. ISBN 0-89871-412-5.

Ernst Hairer, Syvert Nørsett and Gerhard Wanner, Solving ordinary differential equations I: Nonstiff problems, second edition, Springer Verlag, Berlin, 1993. ISBN 3-540-56670-8.
Arieh Iserles, A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, 1996. ISBN 0-521-55376-8 (hardback), ISBN 0-521-55655-4 (paperback).

Numerical partial differential equations

Finite difference methods	Heat Equation and related: FTCS scheme · Crank–Nicolson method Hyperbolic: Lax–Friedrichs method · Lax–Wendroff method · MacCormack method · Upwind scheme · Other: Alternating direction implicit method · Finite-difference time-domain method

Finite volume methods	Godunov's scheme · High-resolution scheme · MUSCL scheme · AUSM · Riemann solver

Finite element methods	hp-FEM · Extended finite element method · Discontinuous Galerkin method · Spectral element method · Meshfree methods · Mortar methods

Other methods	Spectral method · Pseudospectral method · Method of lines · Multigrid methods · Collocation method · Level set method · Boundary element method · Immersed boundary method · Analytic element method · Particle-in-cell · Isogeometric analysis

Domain decomposition methods	Schur complement method · Fictitious domain method · Schwarz alternating method · Additive Schwarz method · Abstract additive Schwarz method · Neumann–Dirichlet method · Neumann–Neumann methods · Poincaré–Steklov operator · Balancing domain decomposition · BDDC · FETI · FETI-DP